Куперс

Умение быстро считать – это необходимый навык любого культурного человека. Базовые арифметические знания пригодятся при расчетах в магазине. Кроме того, развиваются внимание, память, концентрация, а мышление станет более собранным. Математика – сродни магии, здесь все четко и точно. Существует масса методик, как научиться быстро считать в уме, несколько из них разберем подробнее.

С чего начинать тренировку

Математика базируется на 4 простых действиях – сложении, вычитании, умножении и делении. Разобравшись в них один раз, достаточно заниматься по 5-10 минут в день, чтобы намного улучшить уровень счета. Составляющие успешного обучения:

Популярная букмекерка запустила мобильное приложение для Андроид, можно по ссылке абсолютно бесплатно и без регистрации.

• умение концентрировать внимание на поставленной задаче;
• знание основных формул;
• практика.

Начинают с самого простого – сложения однозначных чисел. Как только поиск правильного ответа займет не более 2 секунд, решают примеры с переходом через 10.

Технику называют «опора на десяток», например, складывают 7 и 8:

• сколько не хватает с 7 до 10 – тройки;
• представляют 8 как сумму 3 и второго «куска» – это 5;
• прибавляют к 7 тройку, как недостающее до 10, затем вторую часть (5);
• в итоге получают 15.

Простейшая техника ускорит счет.

Действие сложения

Рассмотрим, как взрослому научиться быстро считать в уме сложение многозначных чисел. Надо уметь складывать одинаковые разряды. Исходные данные разбивают на определенные разряды и складывают – тысячи с тысячами, сотни с сотнями и т.д. Разбивка «по старшинству» ускоряет сложение.

Пример сложения 456 и 789:

Таким же образом считают все многозначные числа.

Сложение и вычитание натуральных чисел базируется на правилах:

Таким образом всегда решают примеры с простыми числами. Техника поможет, если стоит вопрос, как быстро научиться считать сдачу. Ее легко освоит ребенок, знакомый с первыми простейшими действиями – сложение/вычитание.

Действие вычитания

Начинают также с простейших однозначных и двузначных чисел первого, второго десятка. Помогает та же техника с «переходом через 10». Например, следует вычесть из 12 всего 8, действуют так:

• разбивают 12 на 10 и 2;
• из 10 вычитают 8 – равно 2;
• к 2 прибавляют остаток из 12 – тоже 2;
• в итоге получают 4.

Вычитание многозначных чисел немногим сложнее.

К примеру, надо решить 528-326:

1. Разбивают 528 на 500, 20, 8. Исходное 326 разбивают на 300, 20, 6.
2. Вычитают 500-300=200, 20-20=0, 8-6=2.
3. Складывают результат 200+0+2 = 202.

Пример решен.

Совет! Чтобы решить пример с вычитанием из 1000, каждую цифру вычитают из 9, последнюю из 10, результат складывают. Например: 1000-202 = (9-2)+(9-0)+(10-2) = 798.

Действие умножения

Если понимать, что умножение – это сложение одинаковых чисел определенное количество раз, ничего сложного в действии нет. Например, 4*7 = 4+4+4+4+4+4+4. В итоге получают 28. Упростит действие таблица умножения. Ее знает каждый школьник.

На заметку! Самое сложное в таблице действие – умножение 7*8. Тут действует мнемотехническая техника «пять шесть, семь, восемь». В результате умножения 7 и 8 получают 56.

Чтобы правильно умножать числа, их сводят к простым. Рассмотрим техники умножения.

Умножение 9 и 11

Правило при умножении на 9 умножают на 10 и вычитают 9. Если умножают на 11, сначала умножают на 10, прибавляя исходный показатель.

Пример:

• 15*9 = 15*10-15 = 150-15 = 135;
• 57*11 = 57*10+57 = 570+57 = 627.

Интересно! Чтобы возвести в квадрат число, оканчивающееся на 5, умножают десяток на десяток +1 и дописывают 25. Например: 35*35 = 3*(3+1) и дописывают 25 = 1225.

Умножение на 5 чисел до 10

Эта техника поможет правильно умножать двух-, трехзначные числа. Правило простое – множитель делят на 2. Получив результат в виде целого показателя, добавляют в конце 0, а если число не целое, отбрасывают остаток и добавляют в конце 5.

Пример 1482*5 решают так:

Техника, как быстро научиться считать деньги, умножая число на 5, 25, 50, 125 с использованием формул:

• А*5 = А*10/2;
• А*50 = А*100/2;
• А*25 = А*100/4;
• А*125 = А*1000/8.

Приставляя вместо А цифру, в процессе решения формулы получают нужный результат. Например, 25*25 = 25*100/4 = 2500/4 = 625.

Техника умножения на 4

Метод самый простой – исходный показатель умножают на 2, затем итог снова 2. К примеру, 2*4 = 2*2*2.

Умножение больших чисел с одним четным

В этом случае пользуются методикой упрощения множителей. Четное число уменьшают в 2 раза, а нечетное увеличивают в 2 раза. Например, 48*125 = 24*250 = 12*500 = 6*1000 = 6000.

Умножение многозначного числа на однозначное

Разбираясь, как научиться быстро считать деньги на кассе, пользуются техникой раскладывания на порядки, как в случае сложения. Пример 468*6 решают так:

1. Раскладывают 468 на 400, 60, 8. Умножают каждое число на 6.
2. Получают (400*6) = 2400 + (60*6) = 360 + (8*6) = 48. Итого 2400+360+48 = 2808.

Умножение простых чисел

Диагональный метод нужен при поисках техники как быстро научиться считать устно. Заключается способ в дописывании числа, которого «не хватает до 10».

Пример 7*8 решают так:

• высчитают недостающее до 10 – в 7 это 3, в 8 это 2;
• затем 8-3 = 5;
• 3*2 = 6;
• в итоге получают 56.

Умножение чисел от 10 до 20

Умножение двузначных чисел

Упрощают процесс снова разложением двузначных чисел на простые действия. Пример 78*56 решают так:

Пользуясь принципом упрощения и раскладывания больших чисел на разряды, умножают все двузначные числа.

Умножение на 9, 99, 999

Возведение в квадрат

Это тоже умножение, при котором число раскладывают на составляющие. Сначала находят произведение первой цифры на следующую за ней, результат будет заканчиваться на квадрат последней цифры. Пример возведения 75 в квадрат решают так: 7*8 = 56; 5*5 = 25. В итоге 75*75 = 5625.

Техника деления

Математическая формула деления – это «обратное» умножению. То есть при умножении складывали, а при делении вычитают. Чтобы разделить 56 на 7, подбирают число, при умножении которого на 7 в итоге будет 56. Зная таблицу умножения, сделать это просто, искомое число 8.

При делении многозначного числа на однозначное от исходного показателя «отрезают» круглые части, каждая из которых будет делиться на 8, в соответствии с таблицей умножения.

Пример 6144/8 решают так:

В итоге получают 760+8 = 768.

Техника деления на двузначное число

Эта самая гениальная техника, ни на что не похожая. Решая пример 5148/66, делают так:

• подгадывают, в каком десятке будет лежать результат;
• получают 70, поскольку при решении 70*66 = 4620, это самое близкое число к исходному делимому 5148;
• применяют математический закон о последней цифре результата умножения двух чисел – она всегда совпадает с последней цифрой результата умножения;
• получают искомое число, которое при умножении на 66 дает 5148 – это будет окончание на 3 или на 8 (3*6 = 18, 8*6 = 48);
• считают по окончаниям в десятке между 70 и 80 – находят всего два числа 73 и 78;
• теперь умножают 78*66 = 78*60+78*6 = 4680+468 = 500+148 = 5148.

Правильный ответ примера 5148/66 = 78.

Деление на 5, 50, 25

Применяют правило – умножают число на 2 и перемещают запятую на одну цифру назад. Например, 145/5 = 145*2 = 290, смещение запятой назад дает в итоге 29.

При делении на 50, 25 применяют формулы:

• А/50 = А*2/100;
• А/25 = А*4/100.

Например, 2350/50 = 2350*20/100 = 4700/100 = 47 и т.д.

Самые простые техники быстрого счета

Если что-то показалось сложным, есть ряд методик быстрого счета:

Совет! Чтобы умножить на нецелое число (19, 27, 39 и т.д.), сначала умножают на большее целое, затем отнимают исходное число нужное количество раз. Например, 3*39 = 3*40-3 = 120-3 = 117.

Как считать чаевые в процентах

Быстрое определение суммы чаевых – обязательная мера в кафе или ресторане. Иногда в заведениях общепита уже заложены чаевые и тут важно быстро считать, чтобы пользователя не обманули.

Например, вычисление 7% от 300 делают так:

• раскладывают большое число на сотни;
• из каждой 100 считают 7%, это 7;
• складывают количество высчитанных процентов по количеству сотен = 7+7+7 = 21.

Вот и все премудрости. Зная их, взрослый никогда не ошибется в сдаче на кассе, рынке. Также будет просто объяснить правила математики малышу.

Как ребенку научиться быстро считать в уме:

• тренироваться каждый день вместе с родителями;
• считать собственные деньги, затраты.

Тут многое делают родители, отправляя ребенка в магазин и поручая считать сдачу. Быстрее всего учатся считать на деньгах. И именно эти знания затем пригодятся в жизни.

Образец

Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.

Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.

После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).

Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.

Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.

Гаусс и устный счет

Карл Фридрих Гаусс

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.

По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.

В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.

Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.

Сложение чисел в уме

Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.

Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.

Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.

Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084

Вычитание чисел в уме

Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.

Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.

Теперь считаем: 528-300-20-1=228-20-1=208-1=207

Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.

Умножение чисел в уме

Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.

8*4=8+8+8+8=32

Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.

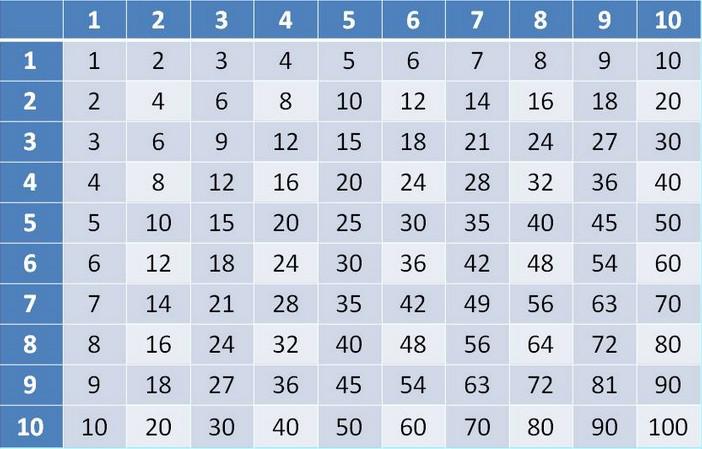Таблица умножения

Умножение многозначных чисел на однозначные

Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.

Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.

• 79*50=(70+9)*50=3500+450=3950
• 79*7=(70+9)*7=490+63=553
• 3950+553=4503

Умножение на 11

Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.

Чтобы умножить двузначное число на 11, две цифры числа складываем друг с другом, и получившуюся сумму вписываем между цифрами исходного числа. Получившееся в итоге трехзначное число — результат умножения исходного числа на 11.

Проверим и умножим 54 на 11.

• 5+4=9
• 54*11=594

Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами — эта хитрость работает!

С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.

Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.

Проверим! Возведем в квадрат число 75.

• 7*8=56
• 5*5=25
• 75*75=5625

Раньше все считали без калькуляторов

Деление чисел в уме

Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.

Деление на однозначное число

При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.

Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:

6144:8=(5600+544):8=700+544:8

Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:

544:8=(480+64):8=60+64:8

Осталось разделить 64 на 8 и получить результат, сложив все результаты деления

64:8=8

6144:8=700+60+8=768

Деление на двузначное число

При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.

При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.

Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.

Сколько будет 4424:56?

Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.

56*80=4480

Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:

79*56=4424

Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

Картина Н.П. Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского»

Полезные советы

В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:

• Не забывайте тренироваться каждый день;
• не бросайте тренировки, если результат не приходит так быстро, как хотелось бы;
• скачайте мобильное приложение для устного счета: так вам не придется самостоятельно придумывать себе примеры;
• почитайте книги по методикам быстрого устного счета. Существуют разные техники устного счета, и вы сможете овладеть той, которая лучше всего подходит именно вам.

Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!