Куперс

Примеры полных и сокращённых имён

Ранее, основываясь на гипотезе, что морфема А в именах древнеегипетских богов Амон и Атум образует развёрнутые и торжественные варианты от, соответственно, Мин и Тум, мне удалось определить значения следующих имён:
Аполлон = Α + πολλός (греч. «сильный», «могущественный»);
Атон = Α + tn (древн.-егип. «это»).
Но самое главное — полностью расшифровано имя Александр Македонский, в котором попутно установлены значения имён Алекс и Андрей:
Алекс = 3rwks (вокализация: ареукс, алеукс; значение в древн.-егип. — «царь», «я — царь»);
Андрей = I + ndrs (древн.-егип. «бог» с окончанием s).
Имя Македонский — это акроним от титула МААТ-КА-АТОН («истинный образ бога солнца»).
И вот совсем недавно обратил внимание, что в знакомых нам именах сохранилась древнейшая традиция образования полных имён с добавлением морфемы А, либо, наоборот, образование сокращённых имён с выпадением указанной морфемы:
Анфиса — Фиса
Аполлинария — Полинария
Артём — Тёма
Афанасий — Панас, Танас
Афиноген — Финоген, Финогей
Аксана — Ксана, Ксюша
Аксинья — Ксения
В следующих примерах всё то же самое происходит с морфемой И. Видимо, как и в древнеегипетском языке она эквивалентна морфеме А:
Иван — Ваня, Жан, Ван
Исидор — Сидор
Исмаил — Сманя, Смаил
Изот — Зот
Израиль — Сруль
Илларион — Ларион
Ираида — Рида, Раида, Риида
Источник большинства примеров имён — АЛФАВИТНЫЙ СПИСОК ИМЕН.

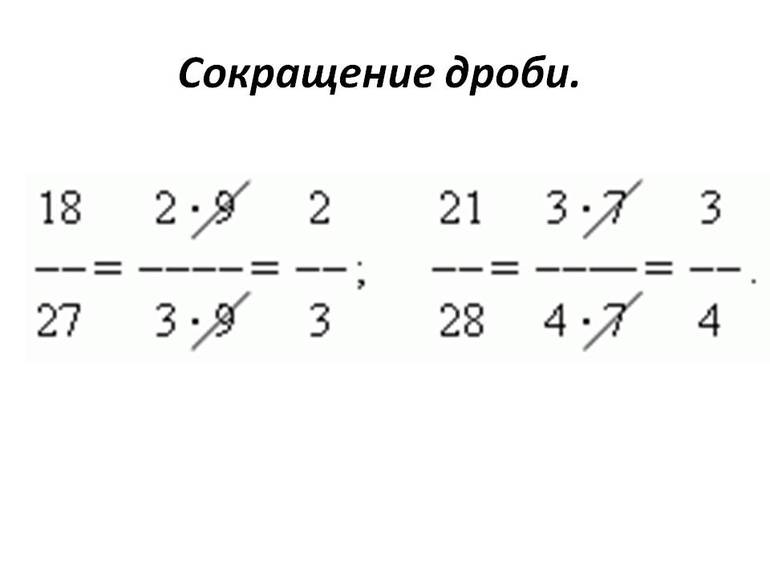
Разберемся в том, что такое сокращение дробей, зачем и как сокращать дроби, приведем правило сокращения дробей и примеры его использования.

Что такое «сокращение дробей»

Сократить дробь

Сократить дробь — значит разделить ее числитель и знаменатель на общий делитель, положительный и отличный от единицы.

В результате такого действия получится дробь с новым числителем и знаменателем, равная исходной дроби.

К примеру, возьмем обыкновенную дробь 624 и сократим ее. Разделим числитель и знаменатель на 2, в результате чего получим 624=6÷224÷2=312. В этом примере мы сократили исходную дробь на 2.

Приведение дробей к несократимому виду

В предыдущем примере мы сократили дробь 624 на 2, в результате чего получили дробь 312. Нетрудно заметить, что эту дробь можно сократить еще. Как правило, целью сокращения дробей является получение в итоге несократимой дроби. Как привести дробь к несократимому виду?

Это можно сделать, если сократить числитель и знаменатель на их наибольший общий делитель (НОД). Тогда, по свойству наибольшего общего делителя, в числителе и в знаменателе будут взаимно простые числа, и дробь окажется несократимой.

ab=a÷НОД(a, b)b÷НОД(a, b)

Приведение дроби к несократимому виду

Чтобы привести дробь к несократимому виду нужно ее числитель и знаменатель разделить на их НОД.

Вернемся к дроби 624 из первого примера и приведем ее к несократимому виду. Наибольший общий делитель чисел 6 и 24 равен 6. Сократим дробь:

624=6÷624÷6=14

Сокращение дробей удобно применять, чтобы не работать с большими цифрами. Вообще, в математике существует негласное правило: если можно упростить какое-либо выражение, то нужно это делать. Под сокращением дроби чаще всего подразумевают ее приведение к несократимому виду, а не просто сокращение на общий делитель числителя и знаменателя.

Слишком сложно? Наши эксперты помогут разобраться

Правило сокращения дробей

Чтобы сокращать дроби достаточно запомнить правило, которое состоит из двух шагов.

Правило сокращения дробей

Чтобы сократить дробь нужно:

1. Найти НОД числителя и знаменателя.
2. Разделить числитель и знаменатель на их НОД.

Рассмотрим практические примеры.

Пример 1. Сократим дробь.

Дана дробь 182195. Сократим ее.

Найдем НОД числителя и знаменателя. Для этого в данном случае удобнее всего воспользоваться алгоритмом Евклида.

195=182·1+13182=13·14НОД(182, 195)=13

Разделим числитель и знаменатель на 13. Получим:

182195=182÷13195÷13=1415

Готово. Мы получили несократимую дробь, которая равна исходной дроби.

Как еще можно сокращать дроби? В некоторых случаях удобно разложить числитель и знаменатель на простые множители, а потом из верхней и нижней частей дроби убрать все общие множители.

Пример 2. Сократим дробь

Дана дробь 3602940. Сократим ее.

Для этого представим исходную дробь в виде:

3602940=2·2·2·3·3·52·2·3·5·7·7

Избавимся от общих множителей в числителе и знаменателе, в результате чего получим:

3602940=2·2·2·3·3·52·2·3·5·7·7=2·37·7=649

Наконец, рассмотрим еще один способ сокращения дробей. Это так называемое последовательное сокращение. С использованием этого способа сокращение производится в несколько этапов, на каждом из которых дробь сокращается на какой-то очевидный общий делитель.

Пример 3. Сократим дробь

Сократим дробь 20004400.

Сразу видно, что числитель и знаменатель имеют общий множитель 100. Сокращаем дробь на 100 и получаем:

Общие сведения

Первые упоминания о дробях встречаются в Древнем Египте. Его жители умели делить два предмета на три части. Применяли они для этого специальное обозначение: 1/2, 2/3, 1/3. При этом запись вида 2/3 была единственной, где в верхней части использовалась не единица, а двойка. Египтяне для обозначения, впрочем, как и вавилоняне, использовали формулу: 1/ n. Для записи других дробей использовалась сумма. Например, вместо 8/15 они использовали сложение двух выражений: 1/3 и 1/5.

Работать с такими дробями было сложно. Различные философы и учёные пытались придумать запись, универсальную для любых случаев. Так, были попытки использовать шестидесятеричные дроби, которыми пользовались в Вавилоне и Греции. Но выполнять над ними операции опять же было сложно. В Риме использовали систему, называемую асс. В её основе лежало деление на двенадцать. Долю, которую она составляла, называли унцией.

Современную же систему записи предложили в Индии. Единственным отличием от общепринятой записи была её перевернутость. Сверху писали делимое, а внизу — делитель. Дробную черту не ставили. Запись же, используемая сегодня, была предложена арабами.

Любая дробь состоит из двух частей: верхней, называемой числителем, и нижней — знаменателя. При произношении читается сначала числитель, а после знаменатель. Например, 3/8 — три восьмых. Верхняя часть обозначает, сколько взято долей, а нижняя — каких. В алгебре используется и иная формулировка. Числитель называют делимым, а знаменатель делителем.

Существуют следующие виды дробей:

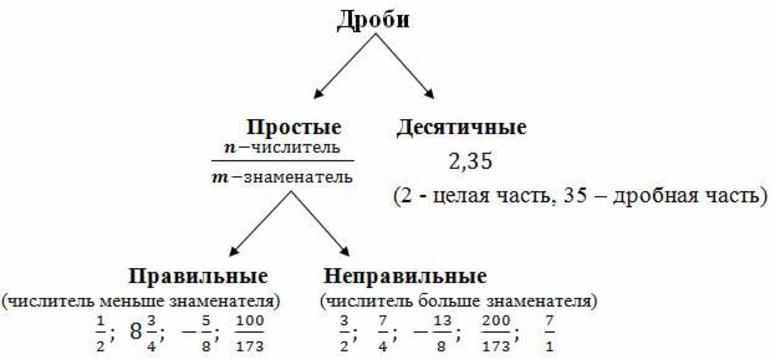
• Обыкновенные — это числа, образованные одной или несколькими равными частями.
• Правильные — отношения, в которых числитель больше знаменателя.
• Неправильные — выражения, в которых числитель больше либо совпадает по значению со знаменателем.
• Смешанные — представляют собой сумму, состоящую из натурального числа и правильного отношения.
• Десятичные — это дроби, в знаменателе которых стоит десять в натуральной степени.

В любом виде отношений могут стоять определённые числа или неизвестные переменные. Поэтому сократить дробь можно как со степенями, так и буквами или цифрами. На правило упрощения содержание делителя и делимого не влияет.

Свойства дроби

По сути, сократить дробь — значит, её упростить. Можно использовать разный алгоритм, но в любом случае применяется основное свойство отношений. Заключается оно в том, что если делитель или делимое умножить на одно и то же число, то количественное значение в ответе не изменится. Это правило справедливо и при замене операции умножения на деление.

Алгебраически свойство можно записать в виде равенства: (q * c) / (r * c) = q / r. Для объяснения этого правила используется следующее доказательство. Пусть имеется равенство (q * r) * c = (c * r) * q. Оно возможно, так как соответствует закону умножения натуральных чисел. При этом учитывается свойство деления, согласно которому, если число разделить на равное ему значение, то результатом действия будет единица. Например, с / с = 1 или 12к/12k = 1. Последнее правило довольно логичное и интуитивно понятное. Если представить, что есть число вещей, равное x, и их нужно разложить на кучки так, чтобы в каждой оказалось x предметов, то очевидно, что получится лишь одна кучка.

Исходя из этих двух правил, можно утверждать, что выражения q * c / r * c и q : c / r : c равны q / r. То есть эти два выражения равны друг другу. На уроках математики в школе предлагают графическую иллюстрацию основного свойства. Пусть есть квадрат, который набран из девяти других квадратов. Каждый из них, в свою очередь, разделён на четыре части. Можно утверждать, что основная фигура поделена на 9 * 4 = 36 частей.

Если закрасить пять больших квадратов другим цветом, то фактически будет окрашено 20 квадратов меньшего размера (4 * 5). Отмеченная область составляет 5/9 от целого квадрата или 20/36, если считать маленькие фигуры. Но так как окрашенная часть одна, то справедливо будет утверждать о верности равенства 5 / 9 = 20 / 36. Вместо чисел 20 и 36 можно подставить их произведения. В итоге получится выражение: 5 / 9 = 5 * 4 / 9 * 4 = 20 * 4 / 36 * 4 = 20 / 36. Что и следовало доказать.

Свойство дроби используется при поиске наименьшего и наибольшего общего знаменателя, а также позволяет упрощать выражения. Невозможно правильно научиться сокращать дроби, не понимая рассмотренного правила.

Алгоритм сокращения

Существующие дроби можно разделить на сократимые и несократимые. Сократить отношение — значит, разделить верхнюю и нижнюю часть на общий делитель. При этом его значение не должно быть равное единице. В итоге получится новое выражение с меньшим значением делителя и делимого. Например, пусть дана дробь 16 / 24. Числитель и знаменатель выражения можно разделить на восемь. В результате запись упростится до вида 16:8 / 24:8 = 2 / 3. Полученная дробь является уже несократимой и её дальнейшее упрощение невозможно.

Любое упрощение выражения можно представить в виде следующего алгоритма:

• нахождение наибольшего общего делителя числителя и знаменателя;
• деление делимого и делителя на найденное число;
• получение несократимой дроби после выполнения операции.

Таким образом, суть действия сводится к нахождению такого сократителя, после применения которого она превратится в тождественную начальной, но уже станет несократимой. Наибольшим общим делителем (НОД) называют одночлен или многочлен, являющийся самым большим из всевозможных делителей, на которое числитель и знаменатель делится без остатка. Например, для чисел 12a и 24a НОД будет равный 12a.

Чтобы быстро найти НОД, нужно знать таблицу умножения и уметь раскладывать числа на простые множители. Ими называют числа, которые делятся на единицу и сами на себя. Существует даже таблица простых чисел до 997, с которой знакомят на уроках алгебры в 7 классе. Но многие натуральные числовые выражения могут делиться и на другие цифры без остатка. Например, двенадцать можно разделить на 1, 2, 3, 4, 6, и 12. Эти числа называют делителями.

При разложении используется запись в виде столбика с вертикальной чертой. В правой части пишут делимое, а в левой — исходное значение. Начинают пробовать делить на двойку, если действие невозможно, повышают значение делимого на единицу. Например, 45 = 3 * 3 * 5.

При поиске НОД каждый знаменатель раскладывают на простые множители, а затем находят одинаковые цифры и перемножают их. Полученный ответ и будет искомым сокращателем. Например, в числителе стоит число 24, а в знаменателе 42. Согласно правилу, их нужно разложить: 24 = 2 * 2 * 2 * 3 и 42 = 2 * 3 * 7. В одной и другой записи повторяются цифры три и два. Их произведение 2 * 3 = 6 и является НОД, на который и будет сокращаться дробное выражение. То есть 24:6 / 42:6 = 4 / 7. Полученная дробь является уже несократимой.

Сложные выражения

Многочлены, стоящие в числителе или знаменателе, имеющие первую степень, сокращать довольно легко. Но часто в задании попадаются степенные выражения. Для того чтобы их упростить, нужно хорошо знать основные формулы и свойства степеней. Заключаются они в следующем:

• При умножении степеней с одинаковым основанием последнее остаётся без изменения, а показатели складываются: i2 * i4 = i6.
• При делении степеней с равным основанием из показателя числителя вычитается степень, стоящая в знаменателе: i4 / i3 = i1.
• Для возведения степени в степень показатели перемножаются: (i2)4 = i8.
• Для того чтобы выполнить произведение в степени, необходимо каждый член, стоящий в скобках, возвести отдельно в указанный показатель: (i * q)n = in * qn.
• Чтобы раскрыть скобки в степени, при делении нужно возвести в степень отдельно числитель и знаменатель: (i / q) n = sn / qn.

Зная эти свойства, можно приступать непосредственно к решению примеров. Например, пусть дано выражение: 147 * 282 / 79 * 24. Для упрощения дроби следует рассуждать следующим образом. Число четырнадцать можно представить как семь, умноженное на два, а двадцать восемь — как семь, умноженное на четыре. То есть, используя свойства степеней, можно записать равенство: 147 * 282 / 79 * 24 = (27 * 77 * 72 * 42) / (79 * 24).

Можно увидеть, что в числителе находится два одночлена с одинаковым основанием. Это две цифры семь, которые можно объединить: (27 * 79 * 42) / (79 * 24). В делимом и делителе теперь находится одинаковое число 79, на которое можно сократить, то есть исключить из формулы. После преобразования выражение примет вид: 27 * 42 / 24. Два в степени семь разделить на два в степени четыре даст в ответе два в степени три. Таким образом, дробь превращается в простой одночлен: 23 * 42 = 23 * 22 * 22 = 27 = 128.

Смотря на этот пример, можно понять важность упрощения дробей. Ведь из задания, практически недоступного для решения, получилось простейшее наглядное выражение. Но при этом может случиться так, что исходная формула будет довольно сложна для предварительного анализа, например, содержать квадратный корень, экспоненту или логарифм. Для таких случаев есть резон использовать специализированные сайты-вычислители.

Использование онлайн-калькулятора

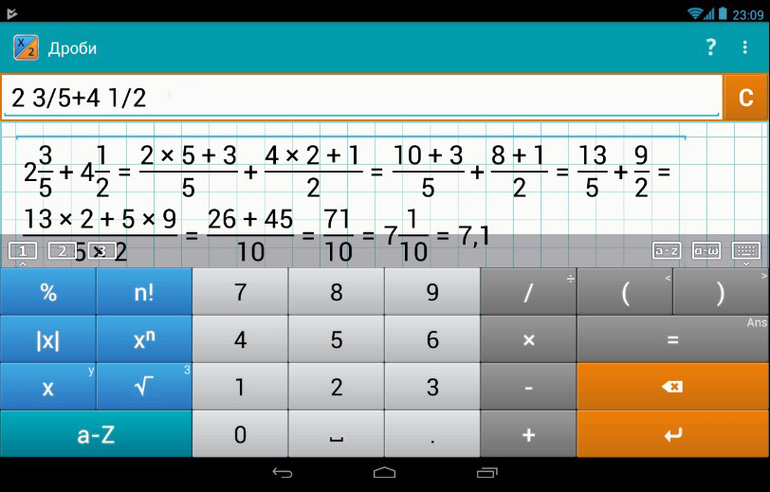
Воспользоваться возможностью сократить дробь на онлайн-калькуляторе сможет любой пользователь интернета. Такую услугу бесплатно предоставляют несколько десятков специализированных сайтов. Неоспоримое их преимущество заключается в быстром и правильном упрощении любого дробного выражения. При этом от пользователя не требуется никаких математических знаний.

Всё что необходимо, это подключение к сети и веб-браузер с поддержкой Flash плеера. Пользователю нужно просто зайти на сайт и в предложенную форму ввести упрощаемую формулу, а затем нажать виртуальную кнопку «Рассчитать». Программа сделает все вычисления самостоятельно, используя оптимальный алгоритм.

Кроме того, на этих сайтах содержится теоретический материал. Он часто подкреплён примерами. Причём даётся не просто ответ, а приводится вся цепочка вычислений, по которой можно разобраться в сути действий.

Из доступных сайтов можно выделить несколько, наиболее популярных среди пользователей:

• Kontrolnaya-rabota. Сервис поддерживает введение выражений, содержащих как буквенные части, так и числовые. После вычисления приводятся не только пошаговые действия, но и даются пояснения к каждой операции.
• Calcs. Сайт имеет простой интерфейс, но в то же время содержит всю необходимую для расчёта информацию. Страницы онлайн-калькулятора не загромождены рекламными баннерами и ненужной информацией. Недостаток его в том, что сайт не понимает степени.
• Calc. Онлайн-расчётчик позволяет сокращать любые виды дробей и находить их части. После введения выражения калькулятор выдаёт ответ буквально за несколько секунд и приводит подробное решение. Калькулятор также позволяет рассчитывать и отрицательные дроби.

Применение онлайн-калькуляторов может стать частью учебного процесса. Учащийся, вводя различные дроби, может воочию видеть нюансы сокращения того или иного вида выражений, а также использовать ресурсы для проверки самостоятельного решения.